深入浅出密码学
第一章 密码学和数据安全导论¶
- 古希腊时代就已经有将文字写成密文的事例，叫斯巴达密码棒（Scytable of Sparta）
-
密码学：
- Cryptography：指的是一种为了达到隐藏消息含义目的而使用的密文书写科学。
- Cyptanalysis：本身就是一种科学，在某些情况下也指一种破译密码体制的技巧。
- 对称算法
- 非对称算法（公钥算法）
- 密码协议：密码协议主要针对的是密码学算法的应用，比如TLS
- \(x\)为明文、\(y\)为密文、\(k\)为密钥、所有可能密钥组成的集合称为密钥空间（key space）
-
简单对称加密：替换密码
- 替换密码的密钥空间虽然很大，但是并不安全，因为可以通过“字母频率分析”来进行破解。
-
定义1.2.1 基本的穷尽密钥搜索攻击或蛮力攻击
假设 \((x,y)\) 表示一对明文和密文对，\(K=\{k_{1},...,k_k\}\) 表示所有可能的密钥 \(k_i\) 组成的密钥空间。蛮力攻击将检查每个\(k_{i} \in K\)，判断以下条件是否满足：
\[ d_{k_i} = x \]如果该等式成立，则意味着找到了一个可能正确的密钥；否则，继续尝试下一个密钥。
-
密码分析
-
Classical Cryptanalysis：
古典密码分析可以理解为从密文 \(y\) 中恢复明文 \(x\)，或反过来，从密文 \(y\) 中恢复密钥 \(k\) 的一种门科。对此，密码分析可分为两类：
- 发现加密方法内部结构的分析攻击
- 将加密算法看作是黑盒，蛮力攻击
-
Implementation Attack：
我们可以通过旁道分析获得密钥，比如测量处理私钥的处理器的功耗。也可以使用信号处理技术从功耗轨迹中恢复出密钥。除功耗外，电磁辐射或算法运行时的行为都隐含着一定的密钥信息，因此也是非常有用的旁道。需要注意的是，Implementation Attack 绝大多数情况下针对的是攻击者可以物理访问（比如智能卡）的密码体制，因此，绝大多数针对远程系统的基于Internet的攻击通常不会考虑这种方法。
-
Social Engineering Attack：
可以通过行贿、勒索、跟踪或侦探等手段来获取密钥。
-
-
定义1.3.1 Kerckhoffs原理
- 可靠的密码体制必须遵守 Auguste Kerckhoffs 在1883年提出的一个假设，即“Kerckhoffs原理”。
-
合适的密钥长度
- 只有在蛮力攻击是已知的最好的攻击方法时，我们才会考虑对称加密算法中的密钥长度问题。
- 对称加密算法和非对称加密算法所要求的密钥长度完全不同。
- 蛮力攻击对称算法需要的时间表：
-
定义1.4.1 模运算
-
等价类：对于一个给定模数m，选择等价类中任何一个元素用于计算的结果都是一样的。
- 示例：
- 余数公式：\(0 \le r \le m-1\)
- 示例：
-
环
-
定义1.4.2 环
-
特性
- 如果环内任何两个数相加或相乘得到的结果始终在环内，那么这个环就是**闭环**。
- 加法和乘法是**可结合**的，即对所有的\(a,b,c \in Z_m\)，都有\(a+(b+c) = (a+b)+c\)和\(a \cdot (b \cdot c)\)。
- 加法中存在中性元素0，使得对每个\(a \in Z_m\)都有\(a+0 \equiv a\ mod\ m\)。
- 环中的任何元素\(a\)都存在一个负元素\(-a\)，使得\(a+(-a) \equiv 0\ mod\ m\)，即加法逆元始终存在。
- 乘法中存在中性元素1，即对每个\(a \in Z_m\)，都有\(a \times 1 \equiv a\ mod\ m\)。
-
不是所有元素都存在乘法逆元。假设\(a \in Z_m\)，乘法逆元\(a^{-1}\)可以定义为：
\[ a \cdot a^{-1} \equiv 1\ mod\ m \]如果元素\(a\)乘法逆元存在，则可以除以这个元素，即：\(b/a \equiv b \cdot a^{-1}\ mod\ m\) - 找出某个元素的逆元比较困难（通常使用欧几里得（Euclidean）），也有一个比较简单的方法： - 当且仅当\(gcd(a, m) = 1\)，一个元素\(a \in Z\)存在乘法逆元\(a^{-1}\)。 - \(gcd(a, m)=1\)：\(a\)和\(m\)的最大公约数为1，即\(a\)和\(m\)互素。 - 对于所有\(a,b,c \in Z_m\)，都有\(a \times (b+c) = (a \times b) + (a \times c)\)，即**分配法**成立。
-
-
定义1.4.3 移位密码
- 由于只有26种不同的密钥（移位长度），因此使用蛮力攻击即可。
- 与替换密码一样，也可以使用字母频率分析方法来破解。
-
仿射密码：与某个数相乘
- 定义 1.4.4 仿射加密
- 解密推导：
-
仿射密码的密钥空间计算：
\[ \begin{aligned} 密钥空间 &= (a可以取的值) \times (b可以取的值)\\ &= 12 \times 26 = 312 \end{aligned} \]
- 定义 1.4.4 仿射加密
第二章 序列密码¶
-
密码编码学的主要领域：
-
对称密码分为：序列密码和分组密码
- 从图中可以看出，序列密码是1位1密，分组密码则是安组加密，图中的组宽度为b。
-
序列密码：单独加密每个位。序列密码分为“同步序列密码”和“异步序列密码”，异步序列密码多了个“密码反馈(Cipher Feedback, CFB)”
-
分组密码：每次使用相同的密钥加密整个明文位分组。
-
序列与分组的区别：
- 现实生活中分组密码的使用比序列密码更为广泛，尤其是在Internet上计算机之间的通信加密中。
- 由于序列密码小而快，所以它们非常合适计算资源有限的应用，比如手机或其他小型的嵌入式设备。序列密码的一个典型示例就是A5/1密码，它是GSM手机标准的一部分，常用语语音加密。但是，序列密码有时也可用于加密Internet流量，例如“RC4”。
- 以前，人们认为序列密码比分组密码要更高效。软件优化的序列密码的高效率意味着加密明文中的1位需要的处理器指令（或处理器周期）更少。对硬件优化的序列密码而言，高效率意味着在相同加密数据率的情况下，序列密码比分组密码需要的门更少（或更小的芯片区域）。然而，诸如AES的现代分组密码在软件实现上也非常有效。此外，有一些分组密码在硬件实现上也非常高效。比如PRESENT，它的效率与紧凑型分组密码相当。
2.1 序列密码¶
-
定义2.1.1 序列密码的加密与解密
-
加密和解密使用相同的函数
\[ \begin{aligned} d_{s_i}(y_i) &\equiv \overbrace{y_i}^{\text{代入加密函数}} + s_i \ mod \ 2\\ &\equiv (x_i + s_i) + s_i \ mod \ 2\\ &\equiv x_i + s_i + s_i \ mod \ 2\\ &\equiv x_i + 2s_i \ mod \ 2\\ &\equiv x_i + 0 \ mod \ 2\\ &\equiv x_i \ mod \ 2 \end{aligned} \] -
为什么可使用简单的模2加法来进行加密？
-
模2加法的真值表：
\(x_i\) \(s_i\) \(y_i \equiv x_i + s_i \ mod \ 2\) 0 0 0 0 1 1 1 0 1 1 1 0 -
上述表格就是一个 异或门，即 XOR
- XOR 函数是完全均衡的
- 密钥序列为\(s_i\)的本质是什么？
- \(s_i\)本身不是密钥位，\(s_i\)对攻击者而言，看起来必须是随机的才具备安全性。
-
-
2.2 随机数¶
-
随机数生成器类别
- TRNG（真随机数生成器）：
- 输出是不可复制的
- 都是基于物理过程
- PRNG（伪随机数生成器）：
- 从一个初始种子值开始通过各种计算得到序列
- 必须拥有良好的统计属性，即它的输出近乎与TRNG相同
- CSPRNG（加密安全的伪随机数生成器）
- 密码学应用
- PRNG的一个特例
- 给定密钥序列中n个连续位，不存在一个时间复杂度位多项式的算法使得成功预测下一个位\(s_{n+1}\)的概率超过50%
- TRNG（真随机数生成器）：
-
定义2.2.1 无条件安全
- 如果一个密码体质在无限计算资源的情况下也不能破译，则说明它是无条件安全的或信息理论上安全的。
-
定义2.2.2 一次一密（OTP）
- 一个序列密码称为一次一密必须满足一下条件：
- 通过TRNG得到密钥序列：\(s_0, s_1, s_2, ...\)
- 只有合法的通信方才知道密钥序列
- 每个密钥序列位\(s_i\)仅适用一次
- 一次一密是 无条件安全 的。
- 一个序列密码称为一次一密必须满足一下条件：
-
定义2.2.3 计算安全
- 如果为破解一个密码体制，最好的已知算法需要至少t个操作，则说明此密码体质是计算安全的。（未知是否有更好的攻击方法）
-
利用PRNG构建密码流是可破解的
-
因为PRNG具备统计属性的，是线性的，比如一个线性同余发生器：
\[ \begin{aligned} S_0 &= seed \\ S_1 &\equiv AS_i + B \ mod \ m, \ i = 0, 1, ... \end{aligned} \] -
那么密钥值应为\((A, B)\)
-
所以，只需要能够知道两对明文和密文对即可获得两个方程，并得到A与B的解：
\[ \begin{aligned} S_2 &\equiv AS_1 + B \ mod \ m\\ S_3 &\equiv BS_2 + B \ mod \ m \end{aligned} \] -
因为得到的\((A, B)\)可能有多个解，因此如果能再获取一对明文和密文对则可以获得唯一解。
-
-
测试TRNG输出序列的统计属性的工具
- Diehard Battery of Tests of Randomness CD, 1995. http://i.cs.hku.hk/~diehard/
- NIST test suite for random number. http://csrc.nist.gov/rng/
2.3 LFSR¶
-
LFSR（线性反馈移位寄存器）：基于移位寄存器的序列密码
- 度（m）为3的LFSR：
-
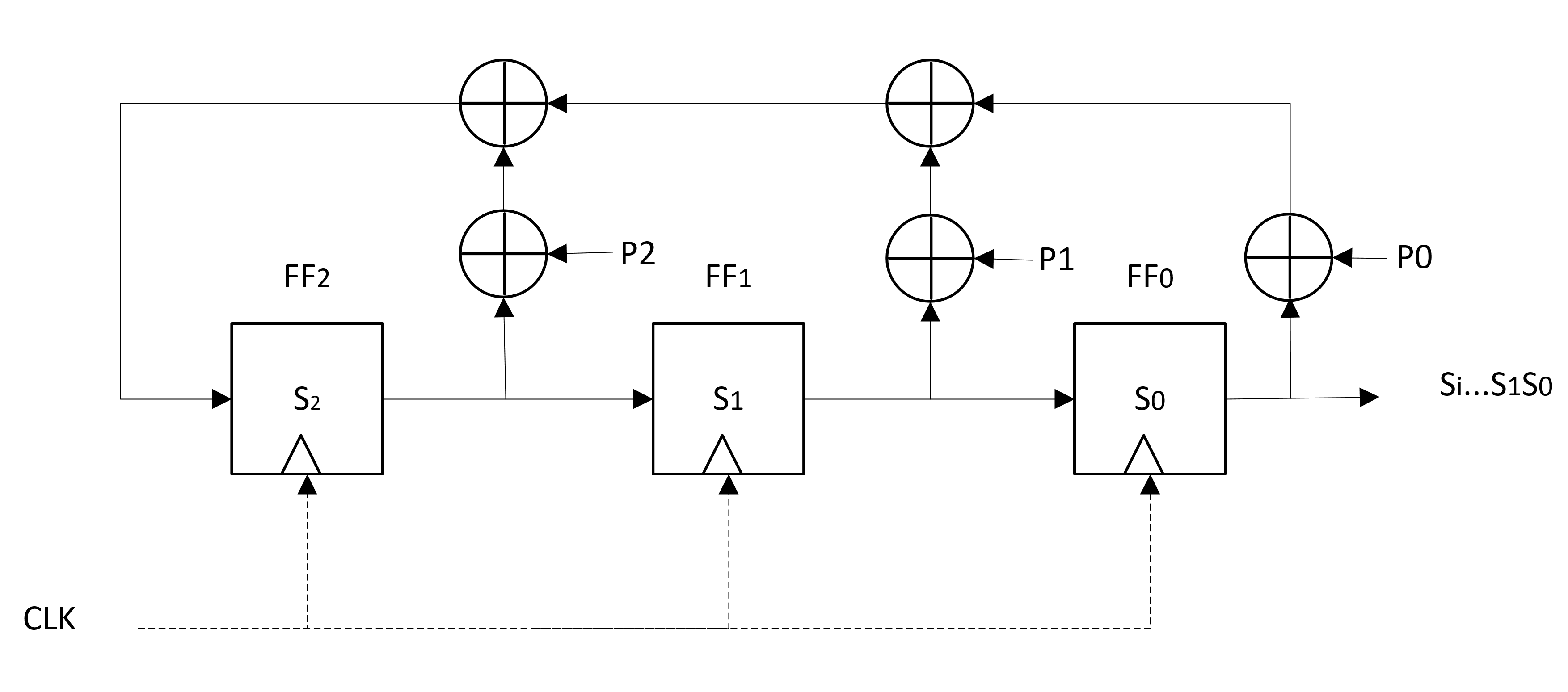
计算方法（仅当\(p_i\)为1时才活跃）
- \(s_i = s_0\)（获取\(s_i\)）
- \(s_0 = s_1\), \(s_1 = s_2\)（更新\(s_1\)和\(s_0\)向右偏移）
- \(s_2 = s_{i-1} \bigoplus s_i\)（计算\(s_2\)）
-
LFSR有时也称为 线性递归。
-
输出计算公式为：
\[ \tag{1} s_m \equiv s_{m-1}p_{m-1} + ... + s_1p_1 + s_0p_0 \ mod \ 2 \]\[ \tag{2} s_{m+1} \equiv s_mp_{m-1} + ... + s_2p_1 + s_1p_0 \ mod \ 2 \]-
归纳后可得：
\[ S_{m + i} \equiv \sum_{j=0}^{m-1} p_j s_{i+j}\ mod \ 2; \ s_i,p_j \in \{0, 1\}; \ i = 0,1,2... \]
-
-
如果反馈系数向量为：\((p_{m-1}, ..., p_1, p_0)\)，则LFSR可以表示为：
\[ P(x) = x^m + p_{m-1}x^{m-1} + ... + p_1x + p_0 \] -
最大长度LFSR拥有 本原多项式（primitive polynomial），该多项式仅有的因子是1和多项式本身。
- 只需要知道2m个输出位就能攻击LFSR（已知明文攻击）
- 是一个很好的拥有良好统计属性但密码学属性非常差的PRNG
- 度（m）为3的LFSR：
-
定理2.3.1 度为m的LFSR可以产生的最大序列长度为\(2^m - 1\)
- 必须排除全部为0的状态，如果LFSR全为0的话，则将一直陷入其中，不可能离开。
2.4 Trivium¶
- 是一个比较新的序列密码，密钥长度为80位。由三个移位寄存器组成，在得到每个寄存器的输出时使用了非线性组件。
- 寄存器长度分别为93，84，111
- 内部结构
- 上面用到的逻辑门都是“与门”
- 注意：AND操作与乘法模2运算等价。如果两个未知数相乘，并且攻击者想恢复寄存器的内容也是未知的，则产生的等式就不再是线性的，因为它们包含了两个未知的乘积。因此AND操作能抵抗发现密码线性特征的攻击。
-
规范
寄存器 寄存器长度 反馈位 前馈位 AND输入 A 93 69 66 91, 92 B 84 78 69 82, 83 C 111 87 66 109, 110 -
加密
- 几乎所有现代序列密码都拥有两个参数：“密钥\(k\)”和“初始向量\(IV\)”
- IV不需要保密，只需要在每次会话时改变就行了。这样的值通常也称为nonces，表示只使用一次的数字。
- 加密阶段
- 初始化阶段：开始时，将80位的IV加载到寄存器A最左边的80个位置和寄存器B最左边的80个位置。除了将寄存器C中最右边3位置为1外，将三个寄存器中其他剩余的位都置为0.
- 热身阶段：在第一阶段中，该密码计时了\(4 \times 288 = 1152\) 次，并没有产生任何密码输出
- 目的：为了充分随机化密码，也确保密钥序列同时取决于密钥\(k\)和\(IV\)。
- 加密阶段：自此阶段开始产生的位就构成了密钥序列，即从第 1153 周期的输出位开始。
第三章 数据加密标准与替换算法¶
3.1 DES简介¶
-
DES：Data Encryption Standard，数据加密标准
- 分组密码
- DES已经不再安全, 最终被AES取代
-
混淆与扩散
- 混淆（Confusion）：是一种使密钥与密文之间的关系尽可能模糊的加密操作。如今实现混淆常用的一个元素就是替换；这个元素在DES和AES中都有使用。
- 扩散（Diffusion）：是一种为了隐藏明文的统计属性而将一个明文符号的影响扩散到多个密文符号的加密操作。最简单的扩散元素就是位置换，它常用于DES中；而AES则使用更高级的Mixcolumn。
-
乘积密码：将若干个加密操作串联起来。
- N轮乘积密码的基本原理，其中每轮都执行一次扩散和混淆操作：
- N轮乘积密码的基本原理，其中每轮都执行一次扩散和混淆操作：
-
现代分组密码常用的分组长度为64位或128位，但如果有一个输入位发生翻转，不同分组长度的分组密码的行为都是一样的。
3.2 DES算法概述¶
- 很多（但不是全部）现代分组密码都使用了Feistel网络（实际上，AES不是Feistel密码）。除了潜在的密码学强度外，Feistel网络的另一个优势就是它的加密过程和解密过程几乎完全相同。
3.3 DES的内部结构¶
-
DES的基本构造元件为初始置换和逆初始置换、实际DES轮及其核心、f函数以及密钥编排（key schedule）
-
初始置换表 \(IP(x)\) 和逆初始置换表 \(IP^{-1}(z)\)
-
f函数：负责混淆和置换
-
Expansion函数
-
Round key：由keyschedule得到的。
-
S-盒
- 首位和末位用来查找行，内部的4个位用来查找列，且行和列的开头都是0，如上图的结果为（3,2）。
- 设计准则：
- 每个S-盒都有6个输入位和4个输出位。
- 任意一个输出位都不应该太接近于输入位的线性组合。
- 如果输入的最高位和最低位都是固定的，只有中间的4个位是可变的，则每个可能的4位输出值都必须只出现一次。
- 对于S-盒的两个输入，如果仅有1位不同，则输出必须至少有两位不同。
- 对于S-盒的两个输入，如果只有中间两位不同，则输出必须至少有两位不同。
- 对于S-盒的两个输入，如果开头的两位不同，但最后两位相同，则输出必须不同。
- 对任意有6位非零差分的输入对，32对输入中至多有8对有相同的输出差分。
- 8个S-盒对应的32位输出的冲突（零输出差异）只有在三个相邻的S-盒的情况下才有可能。
-
S-盒引入了非线性，即：
\[ S(a) \oplus S(b) \ne S(a \oplus b) \] -
剩余的S盒不记录，有需要自行搜索即可。
-
-
置换P
- 置换P将扩散引入到了DES中，因为每个S-盒的4位输出都会进行置换，使得每位在下一轮中会影响多个不同的S-盒。由扩充带来的扩散、S-盒与置换P可以保证，在第五轮结束时的每个位都是每个明文位与每个密钥位的函数，这种行为也称为雪崩效应。
-
密钥编排
- 注意：DES的输入密钥通常是64位，其中每第8个位都作为前面7位的一个奇校验位。没有人清楚以这种方式规范DES的原因。任何情况下，这8个奇校验位都不是真的密钥位，也没有增加密码的安全性。所以可以说DES是一个56位的密码，而不是64位的。
-
注意：从图中可以看出一个关键点，在经过16轮密钥编排后，我们的C0和D0正好旋转了28位，也即\(D_0 = D_{16}\) 和 \(C_0 = C_{16}\)
-
密钥编排的目的：
- 实现16轮置换的方法
- 使56个密钥位的每位都用于不同的轮密钥中；每个密钥位差不多会出现在16个轮密钥中的14个。
3.4 DES解密¶
-
DES的优势：其解密过程与加密过程在本质上是完全相同的。与加密相比，解密过程中只有密钥编排逆转了。
-
逆向密钥编排：\(RS_x\)指的是第\(x\)次向右偏移
-
第一轮获取 \(k_{16}\)
\[ \begin{aligned} k_{16} &= PC \text{-} 2(C_{16}, D_{16}) \\ &= PC \text{-} 2(C_0, D_0) \\ &= PC \text{-} 2(PC \text{-} 1(k)) \end{aligned} \] -
第二轮获取 \(k_{15}\)
\[ \begin{aligned} k_{15} &= PC \text{-} 2(C_{15}, D_{15}) \\ &= PC \text{-} 2(RS_1(C_{16}), RS_1(D_{16})) \\ &= PC \text{-} 2(RS_1(C_{0}), RS_1(D_{0})) \\ \end{aligned} \] -
以此类推，都只是向右偏移，因为是逆向，所有有如下规则：
- 在解密的第一轮中，密钥不移位。
- 在解密的第2、9和16轮中，左右两部分均向右移动1位。
- 在其他的\(k_i\)中，均是向右移动2位。
-
-
Feistel 网络中的解密
\[ (L^d_0, R^d_0) = IP(Y) = IP(IP^{-1}(R_{16}, L_{16})) = (R_{16}, L_{16}) \]-
因此，
\[ \begin{aligned} L^d_0 &= R_{16} \\ R^d_0 &= L_{16} = R_{15} \end{aligned} \] -
次轮的 \(L^d_1\) 和 \(R^d_1\) 的计算如下：
-
首先，
\[ L^d_1 = R^d_0 = L_{16} = R_{15} \] -
接着，
\[ \begin{aligned} R^d_1 &= L^d_0 \oplus f(R^d_0, k_{16}) = R_{16} \oplus f(L_{16}, k_{16}) \\ R^d_1 &= [ L_{15} \oplus f(R_{15}, k_{16})] \oplus f(R_{15}, k_{16}) \\ R^d_1 &= L_{15} \oplus [f(R_{15}, k_{16}) \oplus f(R_{15}, k_{16})] \\ &= L_{15} \end{aligned} \]
-
-
注意：解密过程汇总的所有变量都注明了上标 \(d\)，而加密变量则没有上标。
-
同理，后续的所有解密操作都可以归结为：
\[ \begin{aligned} L^d_i &= R_{16 - i} \\ R^d_i &= L_{16 - i} \end{aligned} \] -
最后，解密结束时有如下结果：
\[ IP^{-1}(R^d_{16}, L^d_{16}) = IP^{-1}(L_0, R_0) = IP^{-1}(IP(x)) = x \]
-
3.5 DES的安全性¶
-
密码攻击可以分为：
- 穷尽密钥搜索攻击（或蛮力攻击）
- 分析攻击
-
针对DES密码强度的批评主要以下两个方面：
- DES的密钥空间太小，即该算法很脆弱，易受蛮力攻击。
- DES S-盒的设计准则是保密的，所以有可能已经存在利用S-盒数学属性的分析攻击，只是此攻击只有DES的设计者知道。
-
因为利用蛮力攻击就可以容易的破解单重DES，因此对大多出应用程序而言，单重DES已经不再适用。
-
定义 3.5.1 穷尽密钥搜索：
输入：至少一个明文密钥对 $(x, y)
输出：满足 \(y = DES_k(x)\) 的 \(k\)
攻击：测试所有 \(2^{56}\) 个可能的密钥，直到以下条件成立：
$$ DES^{-1}_{k_i}(y) = x, i = 0,1,...,2^{56}-1 $$
- 注意：找到错误密钥 \(k\) 的可能性很小——只有 \((\frac{1}{2})^8\) 的几率。错误的密钥 \(k\) 指的是只能正确解密一个密文 \(y\) 而不能正确解密后续的密钥。如果攻击者想排除这样的可能性，必须再使用一个明文-密文对来检查此候选密钥（第五章深入探讨）。
-
单重DES只能用于要求短期安全性（比如几个小时）的应用或被加密数据价值较低的情况。然而，DES变体仍然很安全，尤其是3DES：
- EFF(Electronic Frontier Foundation)于1998年构建了一个硬件机器，叫Deep Crack，它使用蛮力攻击可以在56小时内破解DES，而成本才不到25万美元。
- 2006年，来自德国构建了COPACOBANA（Cost-Optimized Parallel Code-Breaker）机器，破解平均不到7天，且成本仅为1万美元。
-
分析攻击：
- Eli Biham和Adi Shamir发现了 差分密码分析（DC），理论上可以破解任何分组密码。然而事实证明，DES的S-盒可以很好的抵抗这种攻击。
- 线性分析攻击（LC），该攻击在前面攻击LFSR的时候已经提及过。
3.6 软硬件实现¶
- 软件实现：通常指的是在桌面CPU或类似智能卡或手机的嵌入式微处理器上运行DES。
- 硬件实现：指的是在诸如专用集成电路（ASIC）或现场可编程们阵列（FPGA）的IC上运行DES实现。
- DES的一个设计标准就是硬件实现的效率。类似\(E\)置换、\(P\)置换、\(IP\)置换和\(IP^{-1}\)置换的置换操作非常易于硬件实现，因为它们只需要布线而不需要逻辑。
3.7 DES算法替代品¶
- AES(Advanced Encryption Standard, 高级加密标准)目前还没有被成功破译。
- AES是公开竞争的结果，在寻找DES替代算法时，与Mars、RC6、Serpent和Twofish一起入围了。所有这些密码都是密码学安全的，并且非常快，在软件实现上尤其如此。
-
三重DES（3DES）：
- 3DES在硬件实现上非常搞笑，但在软件上却不那么高效。
-
增强DES的另一种方法就是使用“密钥漂白”：
\[ y = DES_{k,k_1,k_2}(x) = DES_k(x \oplus k_1) \oplus k_2 \]- 该简单的修改使得DES更能抵抗穷尽密钥搜索。
-
轻量级密码PRESENT
- 轻量级通常指实现复杂度非常低的算法，尤其指硬件实现方面。比如“Trivium就是，而最有希望的分组密码就是PRESENT，它是专门为类似RFTD标签或其他严格性能或成本限制的常用计算应用而设计的。
- 它是一个“替换-置换网络”（SP网络），并由31轮组成。PRESENT的分组长度为64位，并支持80位和128位两种长度的密钥。
- 由 \(k_i\ (1 \le i \le 32)\) 轮密钥、一个非线性替换层（sBoxLayer）、线性按位置换（pLayer）组成。
-
如上图所示，其伪代码如下:
generateRoundKeys() for i=1 to 31 do addRoundKey(STATE, $K_i$) sBoxLayer(STATE) pLayer(STATE) end for- addRoundKey：在每轮刚开始的时候，轮密钥 \(K_i\) 与当前状态进行XOR操作。
-
sBoxLayer：PRESENT使用单个4位到4位的S-盒。这是追求硬件效能的直接结果，因为这样的S-盒的实现比8位的S-盒的实现更紧凑，S-盒的标识如下所示：
\(x\) 0 1 2 3 4 5 6 7 8 9 A B C D E F \(S[x]\) C 5 6 B 9 0 A D 3 E F 8 4 7 1 2 -
Player：置换层表示如下所示：
\(i\)
\(P(i)\)0
01
162
323
484
15
176
337
498
29
1810
3411
5012
313
1914
3515
51\(i\)
\(P(i)\)16
417
2018
3619
5220
521
2122
3723
5324
625
2226
3827
5428
729
2330
3931
55\(i\)
\(P(i)\)32
833
2434
4035
5636
937
2538
4139
5740
1041
2642
4243
5844
1145
2746
4347
59\(i\)
\(P(i)\)48
1249
2850
4451
6052
1353
2954
4555
6156
1457
3058
4659
6260
1561
3162
4763
63-
上表的置换可以用一下方式表示：
\[ P(i) = \begin{cases} i \cdot 16 \text{ } &mod 63,\ i \in \{0, ..., 62\} \\ 63, &i = 63 \end{cases} \]
-
-
密钥编排(80位)：用户提供的密钥存放在一个密钥寄存器 \(K\) 中，并可以表示为：\(k_{79}k_{78}...k_0\)
-
因为第\(i\)轮中，64位的轮密钥\(K_i\)是由寄存器\(K\)当前内容最左边的64位组成，因此有：
\[ K_i = \kappa_{63}\kappa_{62}...\kappa_{0} = k_{79}k_{78}...k_{16} \] -
对于\(K_1\)来说，因为没有进行过任何的sBoxLayer和pLayer操作，因此是\(k\)最左边64位的副本。而后续的\(K_i\)则有如下操作：
- \([k_{79}k_{78}...k_1k_0] = [k_{18}k_{17}...k_{20}k_{19}]\) ，寄存器\(K\)左移61位
- \([k_{79}k_{78}k_{77}k_{76}] = S[k_{79}k_{78}k_{77}k_{76}]\) ，最左边的4位通过S-盒
- \([k_{19}k_{18}k_{17}k_{16}k_{15}] = [k_{19}k_{18}k_{17}k_{16}k_{15}] \oplus \text{round_counter}\) ，将round_count的值\(i\)与\(K\)的\(k_{19}k_{18}k_{17}k_{16}k_{15}\)位进行XOR操作，其中round_counter最不重要的位在最右边。计数器是一个简单的证书，取值范围位(00001, 00010, ..., 11111)，注意计数器值00001可以得到\(K_2\)，00010可以得到\(K_3\)，以此类推。
- 实现：由于PRESENT的硬件优化设计过于激进，与类似AES的现代密码相比，PRESENT的软件性能不是很具有竞争力。
- PRESENT-80硬件实现大概与1600个门所占的面积等价，加密一个64位明文分组需要32个时钟周期。
-
3.8 讨论¶
- 不少主流的分组密码也是基于Feistel网络，比如AES。Feistel网络的示例包括Blowfish、CAST、KASUMI、Mars、MISTY1、Twofish和RC6。与DES完全不同的密码就是IDEA，它将3种不同的代数结构作为原子操作。
- 其他最近提议的小型分组密码还包括 Clefia、HIGHT、mCrypton
待决问题¶
- 练习题：2.10：做不出来
- 练习题：2.11：求逆矩阵忘记了，等学了后再回来看，这个题目不错，需要记录
对称密码¶
- 替换密码
- 仿射密码
- 移位密码（凯撒密码）
讨论与扩展阅读¶
古典密码与摸运算¶
- 了解古典密码及其在历史中发挥的作用：
- F.L.Bauer. Decrypted Secrets: Methods and Maxims of Cyptology Springer, 4th edition, 2007
- D.Kahn. The Codebreakers. The Story of Secret Writing. Macmillan, 1967
- Simon Singh. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. Anchor, August 2000
- 数论
- 经典入门：
- I.Nivens, H.S.Zuckerman, and H.L.Montgomery. An Introduction to the Theory of Numbers (5th Edition). Wiley, 1991
- K.H.Rosen. Elementary Number Theory, 5th Edition. Addison-Wesley, 2005
- 非数学专业人士，强烈推荐：Jerome A.Solinas.Efficient arithmetic on Koblitz curves. Designs, Codes and Cryptography, 19(2-3):195-249, 2000
- 经典入门：
分组密码¶
- 攻击方法[21,114]
- PRESENT-128密钥编排[29]：
- PRESENT优秀参考文献[29,147]
- DES历史概述[165]
- DES高级技术描述[106]
- DES软件实现[20,106]
- DES硬件实现[169,163]
研究机构和通用文献¶
-
国际密码逻辑研究学会（International Association for Cryptologic Research, IACR）
- 三个会刊：CRYPTO、EUROCRYPT、ASIACRYPT
- 研讨会：加密硬件与嵌入式系统（CHES）、快速软件加密（FSE）、公钥密码学（PKC）、密码学理论（TCC）
-
密码学推荐书籍：
- A.J.Menezes, P.C.van Oorschot, and S.A.VanStone. Handbook of Applied Cryptography. CRC Press, Boca Raton, Florida, USA, 1997
- Henk C.A. van TIlborg, editor. Encyclopedia of Cryptography and Security. Springer, 2005
安全系统设计¶
- 标准
- Common Criteria for Information Technology Security Evaluation. http://www.commoncriteriaportal.org/
- German Federal Office for Information Security (BSI). http://www.bsi.de/english/publications/bsi_standards/index.htm
- Federal Information Processing Standards Publications - FIPS PUBS. http://www.itl.nist.gov/fipspubs/index.htm
- International Organization for Standardization (ISO). ISO/IEC 15408, 15443-1, 15446, 19790, 19791, 19792, 21827
引用¶
- 配套学习资源网站：www.crypto-textbook.com
- 密码工具：https://www.cryptool.org/